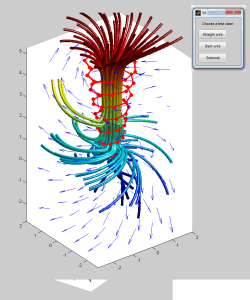
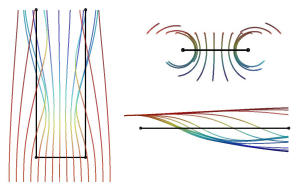Campo magnetico (e velocità indotta da un vortice) lungo una curva generica con MATLAB
Premessa: la lettura di questo articolo potrebbe risultare molto confusa. È talmente specifico che, molto probabilmente, servirà a una persona su un milione. In realtà servirà molto più a me per fissare certe cose che a qualcun altro…
L’induzione magnetica (e la velocità indotta da un vortice, in aerodinamica) è descritta dalla legge di Biot-Savart:
Dove k è una costante moltiplicativa proporzionale all’intensità (della corrente o del vortice). Per questa legge esistono diverse soluzioni analitiche, per i casi più semplici e anche più frequenti: filo rettilineo di lunghezza infinita, solenoide, …
Potrebbe essere interessante osservare il campo magnetico anche per un filo di una forma più strana, come una spirale a passo non costante, o una forma geometrica complessa. Soluzioni analitiche per forme geometriche complesse non ne esistono ed è necessario integrare numericamente la legge di Biot-Savart.
Concettualmente è molto semplice: divido il filo in piccoli intervalli finiti di lunghezza , per ognuno dei quali calcolo l’induzione
e infine ne faccio una sommatoria:
Ecco cosa fa il codice che ho scritto: si assegna un dominio di calcolo (non troppo grande, altrimenti ci impiega un’eternità!) e si fa un ciclo per ogni punto del dominio (tre cicli for su i, j, k). Per ognuno di questi punti, si discretizza la curva in intervalli di ampiezza ds e si calcola l’induzione di ogni elementino sul punto del dominio in questione, sommando i vari contributi (componenti U, V, W).
Non è il massimo dal punto di vista dalle performance, è stata la prima cosa che mi è venuta in mente e non ho neanche pensato se fosse la migliore. Funziona e basta 😀
Un unico appunto lo vorrei fare sull’utilizzo delle meshgrid e del prodotto vettoriale. Il campo magnetico (campo di moto) è descritto da una serie di vettori tridimensionali. Questi vettori dipendono dal punto di applicazione, o meglio, ogni punto del campo ha un suo vettore di induzione, che ne descrive direzione, intensità e verso. In MATLAB, ogni cosa è una matrice e non fanno eccezione i campi vettoriali. Il problema è questo: ogni vettore ha tre componenti, ognuna delle quali è contenuta in una matrice NxNxN. Ho bisogno di tre matrici NxNxN per descrivere il campo vettoriale. Come faccio però a capire in quali punti sono applicati questi vettori?
Qui interviene la funzione meshgrid, che genera una matrice contenente le coordinate dei punti in cui voglio che siano applicati i vettori. Quindi avrò: tre matrici U, V e W contenenti le componenti lungo gli assi x, y e z dell’induzione e tre matrici X, Y e Z contenenti i punti di applicazione dei vettori. Quando si fa il calcolo del di Biot-Savart bisogna tenere presente quanto detto: per il calcolo del vettore R dovrò considerare le matrici X, Y e Z, dato che mi interessa il punto di applicazione del vettore.
Forse era una precisazione banale. Forse no.
Considerazioni aerodinamiche
Il codice permette di integrare la legge di Biot-Savart, che è nota nella fisica per l’induzione di un campo magnetico. In aerodinamica viene invece utilizzata per calcolare la velocità indotta da un vortice. È interessante andare a calcolare il campo di moto nella scia di un’ala utilizzando questo codice.
La Teoria del Filetto Portante di Prandtl ci spiega come sia possibile modellare il campo di moto attorno ad un’ala mediante un sistema di vortici. La schematizzazione più semplice di questo sistema di vortici è il cosiddetto vortice a staffa, di cui rubo senza pietà un’immagine da Google:
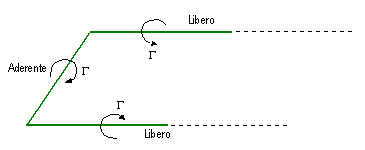
Inserendo nel codice i punti di un vortice a staffa:
L = [-1 6 0;
-1 0 0;
1 0 0;
1 6 0];
Si ottiene un campo di moto di questo tipo:
Non è molto preciso perché è stato calcolato su un dominio di 20 punti, ma rende comunque l’idea.
Se a questo campo di moto sommiamo una corrente uniforme, otteniamo il campo di moto attorno a un’ala:
Il confronto con un’immagine ottenuta per via sperimentale (linee di fumo) mostra la validità di questa teoria:
Download dell’animazione in 3D (.avi, 4.9 MB)
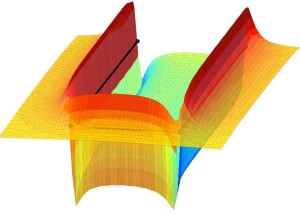
Un’altra figura interessante che è possibile ottenere è quella relativa al downwash:
L’immagine è stata ottenuta utilizzando la funzione surf alla componente verticale della velocità.
Da questa figura si possono notare due cose: la prima è che il vortice parallelo all’ala (vortice aderente) produce un upwash sulla corrente incidente, la seconda è che il downwash è dovuto essenzialmente all’effetto dei vortici laterali (vortici liberi).
Tutte le figure delle linee di corrente sono state ottenute utilizzando la funzione streamtube, che prende in input le mesh, il campo di moto e tre vettori/matrici contenenti i punti da cui devono partire le linee di corrente.
Potete scaricare il codice dal seguente link, o dal file exchange di MATLAB.
Download biot_savart.zip
Download da MATLAB file exchange