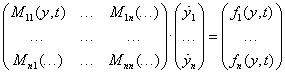Simulatore di Giroscopi in MATLAB
 – Download del codice – eulero.zip
– Download del codice – eulero.zip
Ultimamente ho passato un po’ di tempo a giocare con la funzione ode45 di MATLAB e, dopo aver speso una decina di minuti necessari a capire come impostare i vari parametri di funzionamento, ho iniziato ad integrare tutte le equazioni differenziali che ho incontrato nel corso degli studi.
Tra i vari problemi in cui mi sono cimentato ultimamente, c’è quello delle Equazioni di Eulero, ossia le equazioni che descrivono le rotazioni di un oggetto di forma arbitraria soggetto a dei momenti forzanti. In questo articolo voglio proporre un codice scritto da me che permette la risoluzione di queste equazioni e ne mostra i risultati sottoforma di animazione.
Impostazione del problema
Per prima cosa, impostiamo il problema. Abbiamo un corpo di forma arbitraria nell’ipotesi semplificativa, grazie a opportune simmetrie, di prodotti d’inerzia nulli; chiameremo i momenti principali d’inerzia A, B e C. Questo corpo ha un orientamento nello spazio che è descritto da una terna di angoli di Eulero; in particolare, è stata scelta una sequenza del tipo XYZ e gli angoli sono stati rinominati. Il corpo è soggetto ad un momento le cui componenti attorno agli assi x, y, z, sono state rinominate L(t), M(t), N(t). Le equazioni da risolvere, in questi termini, sono:
La funzione che utilizziamo per integrare le equazioni è, come preannunciato, ode45. Questa funzione accetta in input una function(t,y), il cui valore è il secondo membro di un’equazione differenziale del primo ordine. Il nostro sistema è del secondo ordine, ma è facilmente trasformabile in un sistema del primo ordine utilizzando altre tre equazioni. Chiamando:
Il sistema diventa:
Il codice
– Download del codice – eulero.zip
Per quanto riguarda il codice, questo è diviso in tre file:
- main.m – contenente il codice principale del programma
- eulero.m – contenente il sistema di equazioni da integrare
- ang2dcm.m – funzione che restituisce la matrice dei coseni direttori utilizzata per le rappresentazioni grafiche
Iniziamo dal main.m.
Questa prima parte del codice è molto semplice. Si limita a pulire la memoria, definire due variabili del problema e mostrare un menù di scelta che presenta alcuni casi di problemi preimpostati. L’intero gruppo switch può essere ovviamente rimpiazzato da uno solo dei casi.
Notare che le leggi temporali delle componenti del momento L, M ed N, sono state definite utilizzando le anonymous function, che consistono nell’unico caso in cui è possibile definire una function all’interno di uno script in MATLAB. Queste funzioni sono state definite utilizzando un’altra comodissima routine, che è interp1: questa funzione prende in input (nel nostro caso) due vettori (uno di tempi e uno dei valori del momento) ed uno scalare. Utilizzando una semplice interpolazione lineare permette di restituire un valore della funzione al tempo t, interpolando i valori di M che sono stati forniti a determinati istanti di tempo. In pratica, tu gli dici quanto vale M al tempo 0, 1 e 5, lui ti dice quanto vale M in un qualsiasi istante compreso nell’intervallo [1,5], interpolando linearmente. Le funzionalità di interp1 sono molto più vaste, ma nel nostro caso la utilizziamo semplicemente per questo.
Vediamo ora come impostare il calcolo vero e proprio.
La funzione odeset permette di impostare i parametri relativi all’algoritmo di integrazione. Senza addentrarci troppo nel suo funzionamento, ci limitiamo a settare i parametri di precisione, il cui valore influenza pesantemente il tempo di integrazione.
La funzione waitbar, come dice il nome, permette di creare una barra di caricamento a partire da un valore compreso tra 0 e 1, che nel nostro caso sarà l’intervallo di tempo di integrazione normalizzato. È una funzione comodissima, da quando l’ho scoperta la piazzo praticamente ovunque 😀
La funzione ode45 è quella che effettua l’integrazione. Per il funzionamento nel dettaglio si rimanda all’help di MATLAB, ma per quanto riguarda il nostro problema è sufficiente sapere che accetta in input una funzione (nel nostro caso eulero.m) che restituisce un vettore di sei righe, il cui valore è quello del secondo membro del sistema di equazioni differenziali (opportunamente modificato in modo da avere a primo membro le sole derivate prime delle variabili).
La funzione che andiamo ad integrare dipende dal tempo t, dal vettore di stato y e da una serie di parametri aggiuntivi Par:
Questa funzione viene richiamata ad ogni step di integrazione. Il suo compito è valutare le derivate prime del vettore di stato y. Oltre a fare ciò, questa funzione aggiorna anche la barra di caricamento ad ogni step. In questo modo potremo sapere graficamente a che punto dell’integrazione siamo arrivati.
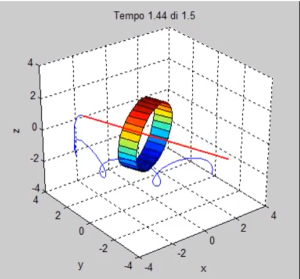
La terza parte del codice, la più divertente, è quella che mostra graficamente i risultati dell’integrazione.
Vengono create due finestre: nella prima viene mostrato l’andamento degli angoli di Eulero, nella seconda l’animazione di un corpo che si muove secondo gli angoli di Eulero trovati.
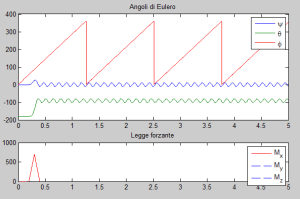
La prima figura è molto semplice. L’unica particolarità è che gli angoli e
vengono limitati agli intervalli [-180, 180] e [0, 360].
 Prima di procedere con l’animazione è necessario conoscere un comportamento peculiare di ode45: insieme al vettore Y contenente le variabili di stato integrate, viene restituito anche un vettore temporale T cui corrispondono gli istanti di tempo relativi ad Y. Questo vettore è, generalmente, non lineare. ode45 ha infatti la capacità di modificare il passo di integrazione rendendolo più o meno fitto a seconda della variazione del vettore di stato. Se utilizzassimo questo vettore senza modificarlo, il risultato sarebbe un video che va piano quando ci sono variazioni irregolari di Y e veloce quando Y è più regolare.
Prima di procedere con l’animazione è necessario conoscere un comportamento peculiare di ode45: insieme al vettore Y contenente le variabili di stato integrate, viene restituito anche un vettore temporale T cui corrispondono gli istanti di tempo relativi ad Y. Questo vettore è, generalmente, non lineare. ode45 ha infatti la capacità di modificare il passo di integrazione rendendolo più o meno fitto a seconda della variazione del vettore di stato. Se utilizzassimo questo vettore senza modificarlo, il risultato sarebbe un video che va piano quando ci sono variazioni irregolari di Y e veloce quando Y è più regolare.
Per ottenere un’animazione fisicamente realistica dobbiamo quindi linearizzare il tempo.
In questo caso, ho deciso di prendere 300 time-step per ogni secondo di simulazione (dovreste metterlo più grande se il vostro computer è performante, più piccolo nel caso contrario). La funzione linspace genera un vettore equidistanziato tra 0 e tfin. La funzione interp1 permette di valutare il vettore di stato in questi nuovi istanti di tempo, interpolando il vettore risultato di ode45.
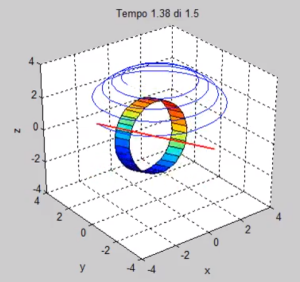
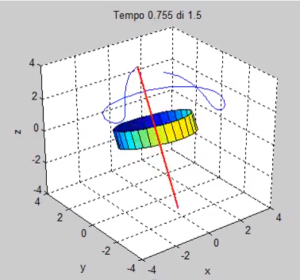
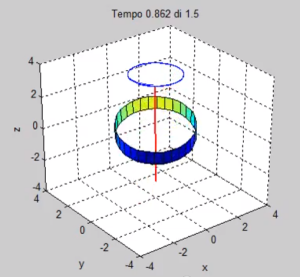
Gli oggetti che vengono rappresentati graficamente sono tre: un cilindro, l’asse del disco e la sua traccia. Il cilindro ha sempre le stesse dimensioni, indipendentemente dai valori dei momenti di inerzia impostati. Ciò può essere fuorviante nel caso in cui A e B siano diversi tra loro (es. case 3), ma non importa.
Sia per la rappresentazione del cilindro che per l’asse, è necessario utilizzare la matrice dei coseni direttori. Questa matrice consente di rappresentare un generico vettore utilizzando gli angoli di Eulero. Per chi avesse installato l’Aerospace Toolbox di MATLAB, esiste una funzione angle2dcm che consente di scrivere una matrice di rotazione per una qualsiasi sequenza di rotazioni.
Dato che non tutti hanno questo strumento, ho aggiunto al codice la funzione ang2dcm, la quale non è altro che una versione semplificata di angle2dcm limitata alla sola sequenza XYZ, che è quella che ho utilizzato.
La traccia dell’asse viene mostrata soltanto per gli ultimi 150 timestep, in modo da non appesantire la rappresentazione grafica.
Nel codice sono presenti una serie di istruzioni commentate riferenti la variabile Mov e la funzione getframe. Questa funzione permette di acquisire l’immagine della figure per poterne creare successivamente un video. Se la utilizzate, tenete presente che richiede molta RAM e rallenta notevolmente il codice.
Assi giunti
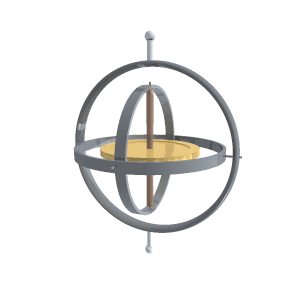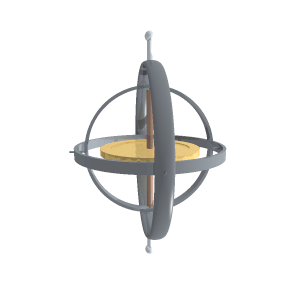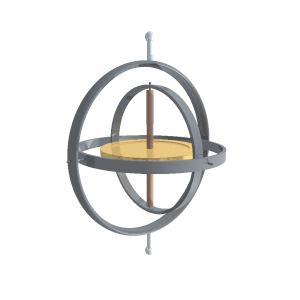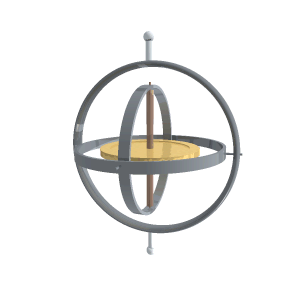 Spesso i giroscopi si studiano utilizzando un sistema di riferimento diverso da quello utilizzato da me. Si considera il giroscopio montato su uno snodo cardanico (vedi figura) e si scrivono angoli e momenti rispetto agli assi degli snodi.
Spesso i giroscopi si studiano utilizzando un sistema di riferimento diverso da quello utilizzato da me. Si considera il giroscopio montato su uno snodo cardanico (vedi figura) e si scrivono angoli e momenti rispetto agli assi degli snodi.
Questa formulazione è molto più conveniente da un punto di vista pratico, ma porta ad una formulazione delle equazioni più articolata. Senza addentrarci troppo nel discorso, la differenza sostanziale nell’utilizzo di ode45 per questo tipo di sistema è che una delle equazioni presenta due termini del secondo ordine. Per questo motivo è necessario impostare mediante odeset una matrice di massa (funzione come al solito di y e t) previa scrittura del sistema in questa forma:
La matrice di massa funziona esattamente come la funzione eulero.m. Notare che nel nostro caso la matrice di massa non è stata impostata, anche se questa corrisponderebbe alla matrice identità.
Video
Ecco infine i video dei 4 case proposti: